Na ovoj lekciji razmotrit ćemo još dvije operacije sa vektorima: vektorski umetnički vektori i mješoviti vektori (odmah vezu, kome treba. Ništa strašno, pa se ponekad događa da je za potpunu sreću, pored toga vektori skalarnog proizvoda, Takođe je potrebno. Takav je ovdje vektorska ovisnost o drogama. Može potražiti dojam da se popnemo u nečistoće analitičke geometrije. Ovo nije istina. U ovom dijelu najviše matematike nema dovoljno drva za ogrjev općenito, osim Pinocchio-a. U stvari, materijal je vrlo čest i jednostavan - teško teško od iste skalarni proizvodČak će i tipični zadaci biti manji. Glavna stvar u analitičkoj geometriji, što mnogi će biti ubijeni ili su već bili uvjereni, a ne varanje u proračunima. Ponavljajte kao čarolija, a vi ćete biti sretni \u003d)

Ako se vektori blistaju negdje daleko kao munje na horizontu, ne problemima, počnite od lekcije Vektori za čajnikeZa obnavljanje ili ponovno nabavljanje osnovnih znanja o vektorima. Za pripremljenijih čitalaca mogu se upoznati sa podacima selektivno, pokušao sam prikupiti najpotpuniju prikupljanje primjera koji se često nalaze u praktičnom radu.

Šta odmah molim? Kad sam bio mali, tada sam znao žonglirati dvije, pa čak i tri kuglice. Spretno naslijedio. Sada uopšte nećete morati žonglirati, jer ćemo razmotriti samo prostorni vektori, a ravni vektori sa dvije koordinate ostat će prekomjerni. Zašto? Ove akcije su rođene - vektorski i mješoviti proizvod vektora definirani su i rade u trodimenzionalnom prostoru. Već lakše!

U ovoj operaciji sudjelujte na isti način kao i u skalarnom proizvodu dva vektora. Neka to bude besmislena pisma.

Akcija sama označava Na sledeći način :. Postoje i druge opcije, ali nekada sam označio vektorski umjetničko djelo vektora baš tako u kvadratnim zagradama sa krstom.

I odmah pitanje: ako u vektori skalarnog proizvoda Uključeni su dva vektora, a ovdje se dvije verzije pomnožene, onda koja je razlika? Izričita razlika, prije svega, kao rezultat:

Rezultat skalarnog proizvoda vektora je broj:

Rezultat vektorskih umjetničkih vektora je vektor:, To jest, množimo vektore i ponovo dobijamo vektor. Zatvoreni klub. Zapravo, otuda i ime operacije. U raznim literaturom za učenje, oznake se mogu varirati, koristiću pismo.

Definicija vektorske umjetnosti

Prvo će biti definicija sa slikom, a zatim komentari.

Definicija: Vektorski rad nolyllyLine Vektori, uzeta u ovom nalogu, nazvan vektor, dužina što je numeričko jednak kvadratu paralelogramaizgrađen na ovim vektorskim podacima; vektor ortogonalni vektori I usmjeren je tako da osnova ima pravu orijentaciju:

Rastavljamo definiciju kostiju, ima puno zanimljivih stvari!

Dakle, možete odabrati sljedeće bitne trenutke:

1) Izvorni vektori označeni crvenim strelicama po definiciji ne kolinoar. Slučaj kolinoarnih vektora bit će prikladan da razmotri malo kasnije.

2) Vektori uzeti u strogo definiranom nalogu: – "A" se pomnože sa "Budite", ne "biti" na "a". Rezultat vektora za umnožavanje vektora To je vektor koji je naveden u plavoj boji. Ako se vektori pomnože sa obrnutim redoslijedom, tada se postavljamo jednakim dužini i suprotnom vektoru (boja maline). To jest jednakost je tačna .

3) Sada se upoznamo sa geometrijskim značenjem vektorskog proizvoda. Ovo je vrlo važna tačka! Dužina plavog vektora (i stoga je vektor maline) numerički jednak kvadratu paralelograma ugrađenog u vektore. Na slici je ovaj paralelogram zasjenjen crnom bojom.

Bilješka : Crtež je shematski, a naravno, nazivna dužina vektorskog proizvoda nije jednaka području paralelograma.

Sjećamo se jednog od geometrijskih formula: područje paralelograma jednaka je proizvodu susjednih strana na uglu između njih. Stoga se na osnovu prethodnog, formula za izračunavanje dužine vektorskog proizvoda:

Naglašavam da u formuli govorimo o dužini vektora, a ne o vrlo vektoru. Šta je praktično značenje? A značenje je da se u zadacima analitičke geometrije područje paralelograma često nalazi kroz koncept vektorske umjetnosti:

Dobit ćemo drugu važnu formulu. Dijagonala paralelograma (crvena točka) dijeli ga u dva jednaka trougla. Shodno tome, područje trokuta, ugrađeno u vektore (crveno izlijevanje), može se naći kod formule:

4) Ništa manje važna činjenica je da je vektor ortogonalni vektori, odnosno . Naravno, suprotno usmjeren vektor (arrow maline) je i pravokutna u originalnim vektorima.

5) vektor je usmjeren tako da osnova Ima pravo Orijentacija. U učionici O. prelazak na novu osnovu Razgovarao sam detaljno o tome orijentacija avionaA sada ćemo se baviti orijentacijom prostora. Objasnit ću vam prstima desna ruka. Mentalno kombinirati kažiprst Sa vektorom I. srednji prst Sa vektorom. Neimenovani prst i mali prst Pritisnite dlan. Kao rezultat palac - Vektorska umjetnost će podići pogled. Ovo je desno bljeska (na slici je on). Sada promijenite vektore ( indeks i srednji prsti) Mjesta, kao rezultat, palac se odvija, a vektorski rad već će pogledati dolje. To je takođe redovno osnova. Možda imate pitanje: Koja osnova radi lijeva orijentacija? "Ime" isti prsti lijeva ruka vektori i dobivaju lijevu osnovu i lijevu orijentaciju prostora (U ovom slučaju palac će biti smješten u smjeru donjeg vektora). Figurativno govoreći, ove baze "zavrti" ili orijentiraju prostor u različitim smjerovima. A ovaj koncept ne bi trebao smatrati nešto zapaljeno ili sažetak - tako, na primjer, orijentacija prostora mijenja se najbijnije ogledalo, a ako "povučete refleksni objekt iz točaka." Neće ga moći kombinovati u Generale. Usput, donesite tri prsta u ogledalo i analizirajte odraz ;-)

... Kako je dobro da sada znate pravo i levo orijentirano Baze, za strašne izjave nekih predavača o promjeni orijentacije \u003d)

Vektorski umetnički rad kolinoarnih vektora

Definicija je detaljno rastavljena, ostaje da saznate šta se događa kada su kolorinerski vektori. Ako su vektori koloriče, tada se mogu postaviti na jednu ravnu liniju i naš paralelogram također "navijaju" u jedan ravan. Područje ovoga, kao matematika kažu, degeneriran Paralelogram je nula. Iz formule se slijedi - sinus nula ili 180 stepeni je nula, a samim tim i područje je nula

Dakle, ako i . Imajte na umu da je sam vektorski proizvod nula vektor, ali u praksi se često zanemaruje i napisano da je i nula.

Privatni slučaj - vektorski vektor proizvoda na sebi:

Uz pomoć vektorskog proizvoda, kolibranost trodimenzionalnih vektora može se provjeriti, a ovaj zadatak ćemo također pogledati između ostalog.

Za rješavanje praktičnih primjera može zahtijevati trigonometrijska tablicaDa biste ga pronašli vrijednosti sinusa.

Pa, zapalite vatru:

Primjer 1.

a) Pronađite duljinu vektorskih vektora za umjetnike ako

b) Pronađite kvadrat paralelograma ugrađenog u verzije ako

Odluka: Ne, ovo nije tipica, početni podaci u uvjetima klauzule namerno sam napravio isto. Jer donošenje odluka bit će različite!

a) Pod uslovom koji trebate pronaći dužina Vektor (vektor umjetnost). Prema odgovarajućoj formuli:

Odgovoriti:

Kohl je ubrzo pitao o dužini, a zatim u odgovoru, navedite dimenziju - jedinice.

b) pod uslovom potrebnom za pronalaženje područje Paralelogram ugrađen u vektore. Područje ovog paralelograma je numerički jednaka dužini vektorskog proizvoda:

Odgovoriti:

Imajte na umu da se u odgovoru na vektorski proizvod govora uopće ne ide, pitali su nas trg figure, u skladu s tim, dimenzija su kvadratne jedinice.

Uvijek gledamo šta je potrebno po stanju, i na osnovu toga formuliramo jasan Odgovor. Može se činiti ključnim, ali ima dovoljno tastera među nastavnicima, a zadatak s dobrim šansama vratit će se u profinjenost. Iako ovo nije posebno rastegnuta Quarid - ako je odgovor netočan, čini se da osoba ne razumije jednostavne stvari i / ili ne u suštini zadatka. Ovaj trenutak treba uvijek biti na kontroli, rješavajući bilo koji zadatak u višoj matematici i u drugim subjektima.

Gdje je bila velika bucchka "en"? U principu, mogao bi se dodatno pridružiti rješenju, ali da bi se smanjio zapis, nisam. Nadam se da svi razumiju da je ovo imenovanje istog.

Popularni primjer za samoposluživanje:

Primer 2.

Pronađite područje trokuta izgrađenog u vektorima ako

Formula za pronalazak tugođeg područja kroz vektorsku umjetnost data je u komentarima na definiciju. Rješenje i odgovor na kraju lekcije.

U praksi je zadatak zaista vrlo čestan, trouglovi uglavnom mogu mučiti.

Da biste rešili ostale zadatke, trebat će nam:

Svojstva vektorskih umjetničkih djela

Međutim, neka svojstva vektorskog rada koji smo već razmotrili, uključit ću ih na ovaj popis.

Za proizvoljne vektore i proizvoljne brojeve, sljedeća svojstva su fer:

1) U ostalim izvorima informacija, ovaj predmet obično nije identificiran u nekretninama, ali vrlo je važno u praktičnim uvjetima. Stoga neka bude.

2) - Nekretnina se takođe rastavlja, ponekad se zove anti-komutativni. Drugim riječima, redoslijed vektora važno je.

3) - tmurno ili asocijativni Zakoni vektorskog rada. Konstante su privremeno izvedene iz vektorskog rada. Zaista, šta oni rade tamo?

4) - distributivna ili distribut Zakoni vektorskog rada. Sa otkrivanjem nosača nema problema.

Kao demonstracija, razmislite o kratkom primeru:

Primjer 3.

Pronađite ako

Odluka: Pod uslovom je potrebno ponovo pronaći dužinu vektorskog proizvoda. Donosimo minijaturnu:

(1) Prema asocijativnim zakonima, izdržimo konstante za preraspodjelu vektorskog rada.

(2) Izdržavamo konstanta izvan modula, dok modul "jede" znak "minus". Dužina ne može biti negativna.

(3) Dalje je razumljivo.

Odgovoriti:

Vrijeme je da bacimo drva za ogrjev u vatru:

Primjer 4.

Izračunajte područje trokuta izgrađenog u vektorima, ako

Odluka: Trokut trg pronađite formulu . Snag je da su sami vektori "CE" i "de" predstavljeni kao sumi vektora. Algoritam je ovdje standardno i nešto podseća na primjere broj 3 i 4 lekcije Vektori skalarnog proizvoda. Rješenje za jasnoću za probijanje u tri faze:

1) u prvom koraku izražavamo vektorski proizvod kroz vektorsku umjetnost, u stvari, express vektor putem vektora. O duljinama nije riječ!

(1) Zamjenjujemo izraz vektora.

(2) Koristeći distributivne zakone, otkrivaju zagrade prema pravilu množenja polinoma.

(3) Koristeći asocijativne zakone, izdržimo sve konstante izvan vektorskih radova. Pod malim iskustvom, 2 i 3 mogu se izvoditi istovremeno.

(4) Prvi i posljednji izraz je nula (nula vektor) zahvaljujući ugodnom objektu. U drugom mandatu koristimo nekretninu protiv komutativnosti vektorskog rada:

(5) Dajemo takve komponente.

Kao rezultat toga, vektor se ispostavilo da se izražava putem vektora, što je potrebno postići:

2) Na drugom koraku ćemo pronaći dužinu vektorskog proizvoda koji vam je potreban. Ova radnja podseća na primjer 3:

3) Pronađite područje željenog trougla:

Faze 2-3 rješenja mogla bi se organizirati s jednom linijom.

Odgovoriti:

Razmatrani zadatak dovoljno se širi u testovima, evo primjera za neovisnu odluku:

Primjer 5.

Pronađite ako

Kratko rješenje i odgovor na kraju lekcije. Da vidimo koliko ste pažnja prilikom proučavanja prethodnih primjera ;-)

Vektorski umetnički rad vektora u koordinatama

definirano u ortonormalnoj osnovi formula se izražava:

Formula i istina Sprydskaya: U gornjem retku odrednice bilježimo koordinatne vektore, u drugoj i trećim linijama "stavi" koordinate vektora i uklapaju se u strogom nalogu - Prvo, koordinate vektora "ve", zatim koordinate vektora "Dubl-mi". Ako se vektori trebaju pomnožiti u različitom redoslijedu, tada bi redovi trebali biti zamijenjeni u mjestima:

Primjer 10.

Provjerite da li će Collinear biti sljedeći svemirski vektori:
ali)
b)

Odluka: Ček se zasniva na jednoj od izjava ove lekcije: ako je kolinovski vektori, a zatim njihov vektorski proizvod je nula (nula vektor): .

a) Dobrodošli vektorsku umjetnost:

Dakle, vektori nisu kolinore.

b) Pronađite vektorsku umjetnost:

Odgovoriti: a) ne Collinear, b)

Ovo je možda sve osnovne informacije o vektorskom proizvodu vektora.

Ovaj dio neće biti vrlo velik, jer se zadaci u kojima se mješoviti proizvod vektora koristi, malo. U stvari, sve će biti ograničeno u definiciju, geometrijsko značenje i nekoliko radnih formula.

Mješovita umjetnička djela vektora je djelo od tri vektora.:

Tako su ih postrojili vlakom i čekaju, ne bi čekali kad su izračunali.

Prvo, opet definicija i slika:

Definicija: Mješoviti posao nekomplenar Vektori, uzeta u ovom nalogu, zvani jačinu paralelepipeda, izgrađen na podacima vektora, opremljen znakom "+", ako je osnova u pravu, a znak "-", ako je osnova ostavljena.

Izvršite sliku. Nevidljive linije zamućene isprekidanom linijom:

Uronite se u definiciju:

2) Vektori uzeti u određenom redoslijedu, odnosno preuređivanje vektora u radu, kako pogađate, ne prolazi bez posljedica.

3) Prije komentiranja geometrijskog značenja, primijetit ću očiglednu činjenicu: mješoviti vektori su broj:. U obrazovnoj literaturi dizajn može biti nešto drugačiji, nekada sam potpisao mješoviti proizvod kroz proračun slova "PE".

A-Prioring mješovita djela je paralelepipipana volumenaIzgrađen u vektorima (brojka se čisti crvenim vektorima i crnim linijama). To jest, broj je jednak volumen ove paralelepiped.

Bilješka : Crtež je shematski.

4) Nemojmo ponovo pariti konceptom orijentacije osnova i prostora. Značenje završnog dijela je da se u jačinu može dodati minus znak. Jednostavne riječi, mješoviti proizvod može biti negativan:.

Neposredno iz definicije slijedi formula za izračunavanje volumena paralelepiped, ugrađen u vektore.

Definicija. Vektor vektora A na vektoru B naziva se vektor koji je označen simbolom [", b] (ili LXB), takav da je dužina vektora [A, B] jednaka (p, gde je y je ugao između vektora A i B (Sl.31); 2) vektor [A, B) okomit na vektore A i B, I.E. okomito u ravninu ovih vektora; 3) Vektor [A, B] je usmjeren tako da je od kraja ovog vektora najkraća rotacija od A do B vidljiva u smjeru suprotnom od kazaljke na satu (Sl. 32). Sl. 32 Sl.31 Drugim riječima, vektori A, B i [A, b) čine pravi putnik, tj. Smješten kao veliki, indeks i srednji prsti desne ruke. Ako su vektori A i B Collinear, pretpostavljamo da je po definiciji dužina vektorskog proizvoda numerički jednaka prostoru sa paralelogramom SA (Sl. 33), izgrađena na varijabilnim vektorima A i B kao Sa strana: 6.1. Svojstva vektorskog rada 1. Vektorski proizvod je jednak nulti vektoru i tek kada je barem jedan od varijabilnih vektora nula ili kada su ovi kolorinerski vektori (ako su vektori A i B Collineear, a zatim ugao između njih, tada je ili 0 ili 7g). Lako je dobiti od činjenice da ako brojite nultu vektor sa cinkonima bilo kojeg vektora, stanje kolibranosti vektora A i B može se izraziti tako 2. Vektorski proizvod je anti-komutativan, i.e. uvijek. U stvari, vektori (A, B) i imaju istu dužinu i Collinear. Smjerovi ovih vektora su suprotno su suprotno zbog kraja vektora [A, b] najkraću rotaciju od A do B bit će viđena u smjeru kazaljke na satu, a od kraja vektora [B, A] - u smjeru kazaljke na satu (B, A]) Sl. 34). 3. Vektorski proizvod ima nekretninu za distribuciju u odnosu na dodatak. 4. Numerički multiplikator mogu se napraviti za znak vektorskog proizvoda 6.2. Vektorski proizvod vektora navedenih koordinatama puštaju vektore i također postavljaju njihove koordinate u bazi. Korištenje distribucijske imovine vektorskog proizvoda nalazimo vektorski proizvod vektora koji su dali koordinate. Mješoviti posao. Popravljamo vektorske radove koordinatnih orma (Sl. 35): Stoga za vektorski proizvod vektora A i B dobivamo iz formule (3) sljedeća izraz formula (4) mogu se napisati u simboličkom, lako pamtiti Obrazac, ako koristite odrednicu trećeg reda: Raspadajući ovo odrednica za elemente 1. linije, dobivamo (4). Primjeri. 1. Pronađite područje paralelograma ugrađenog u vektor željenog područja tako da ćemo pronaći \u003d odakle 2. Pronađite područje trokuta (Sl. 36). Jasno je da je područje B "D Trokut jednak polovini kvadratnog paralelograma o AU V. Izračunavanju vektorskog proizvoda (A, B | vektori A \u003d OA i B \u003d Oh, dobivamo napom. Vektorski proizvod je a ne saradništvo, tj. jednakost ((a, b), c) \u003d [a, | b, c)) u općem slučaju nije tačan. Na primjer, kada je A \u003d SS j, imamo § 7. Mješoviti proizvod Vektori ih pusti tri vektora A, B i s. Uskoro premjestite vektore A i 1\u003e. Kao rezultat toga dobijamo vektor [a, 1\u003e]. Pomnožite je skalarni za vektor C: (k b), c). Broj ([A, B], E) naziva se mješovitim proizvodom vektora A, b. sa i naznačenim simbolom (A, 1), E). 7.1. Geometrijsko značenje mješovitih radnih vektora A , B i iz potrošene točke o (Sl. 37). Ako su sva četiri boda oh, a, b, c leže u istoj ravnini (vektori A, B i C u ovom katalu), zatim mešoviti proizvod ( [A, B], C) \u003d 0. To slijedi iz činjenice da se vektor [A, B | perpendikula u avion u kojem su vektori A i 1 predvideni ", pa, vektor sa. / ako t TOČKE O, A, B, C ne leže u istoj ravnom kosti (vektori A, B i sa nekompletnijom), gradimo na ivicama OA, OB i Paralelepiped (Sl. 38 a). Definicijom vektorskog proizvoda imamo (A, B) \u003d tako sa, gdje je tako i područje oadb paralelogram, a C je jedan vektor, okomit na vektore A i B i takav da je trojka a, b, c - desno , tj Vektori A, B i C nalaze se, odnosno veliki, indekse i srednji prsti desne ruke (Sl. 38 b). Pomnožavanje oba dijela posljednje jednakosti na desni skalar u vektor C, dobivamo da vektorski proizvod vektora navedenih koordinata. Mješoviti posao. Broj RGS C jednak je visini Hgraniranog paralela, snimljen sa znakom "+", ako ugao između vektora sa i sa akutnim (Troika A, B, C - desno), i sa znakom "-" , ako je ugao glup (Trojka A, B, s - lijevo), tako da se na taj način miješaju proizvode vektora A, B i jednak zapreminu v paralelepiped, izgrađen na ovim vektorima kao na ripsu, ako je Trojka A, B, C - desno, i -v, ako trojka a, b, s - lijevo. Na osnovu geometrijskog značenja mješovitog rada, može se zaključiti da umnožavajući TC vektore A, B i C u bilo kojem drugom redoslijedu, uvijek ćemo primiti ili +7 ili -K. Znak proizvodnje. 38 Održavanje ovisit će samo zato što trojke formiraju varijable vektore - desno ili lijevo. Ako vektori A, B, s pravom trojkom, tada su u pravu triogy B, C, A i C, A, B. Istovremeno, sve tri trupe B i, sa; A, S, B i S, B, A - lijevo. Dakle, (A, B, C) \u003d (B, S, A) \u003d (S, A, B) \u003d - (B, A, C) \u003d - (A, S, B) \u003d - (S, B, ali). E ESHERARE Naglašavamo da je mješoviti proizvod vektora jednak Nuduchoga samo kada varijabilni vektori A, B, s kompanijom: (A, B, s kompanijom) 7.2. Mješoviti rad u koordinatama pušta vektore A, B, postavljaju njihove koordinate na osnovu I, J, K: A \u003d (X \\, y \\, z]), b \u003d (x2, y2\u003e z2), c \u003d (x3, uz, 23). Pronalazimo izraz za njihov mješoviti rad (A, B, C). Imamo mješoviti proizvod vektora koji su koordinate dali u bazi I, J, K, jednak odrednicama trećeg reda, čiji su redovi čiji su sačinjeni u skladu s koordinatama prve, druge i trećine varijabilnih vektora. Potrebno i dovoljan uvjet za pratiocu vektora i y \\, z |), b \u003d (h u2. 22), c \u003d (zhz, uz, 23) bit će zabilježeni na sljedeći način | Z, AG2 Y2 -2 \u003d 0. Ultra primer. Provjerite jesu li vektori "\u003d (7,4,6), b \u003d (2, 1,1), c \u003d (19, ii, 17). Vektori koji se razmatraju ili će se međusobno koristiti ovisno o tome da li će biti nula ili ne postoji odrednica da ga raspada u skladu s elementima prvog niza, dobivamo d \u003d 7-6- 4- 15 + 6-3 \u003d 0 ^ - vektori n, b, sa kompasarom. 7.3. Dvostruki vektorski proizvod Dvostruki vektorski proizvod [A, [B, C]] Vektor je okomit na vektore A i [B, C]. Stoga leži u ravnini vektora B i C i mogu se razgraditi na tim vektorima. Može se pokazati da je formula valjana [a, [!\u003e, S]] \u003d b (a, e) - sa (a, k). Vježbe 1. Tri vektora av \u003d c, f? \u003d O i ca \u003d b poslužite kao stranice trougla. Izričite putem A, B i sa vektorima koji se podudaraju sa medijanima am, DN, CP Trougle. 2. Kakvo bi se uvjet trebao vektor p i q biti povezani sa vektorom p + q podijeljen ugao između njih na pola? Pretpostavlja se da se sva tri vektora pripisuju generalnom početku. 3. Izračunajte dužinu dijagonala paralelograma izgrađenog u vektorima A \u003d 5p + 2Q i B \u003d P - 3Q, ako je poznato da | P | \u003d 2V / 2, | Q | \u003d 3 h- (p7ci) \u003d f. 4. Preračunavanje romba kao i b strane romba dokazuju da su dijagonalno romb međusobno okomit. 5. Izračunajte skalarni proizvod vektora A \u003d 4i + 7J + 3K i B \u003d 31 - 5J + K. 6. Pronađite jedinicu vektor A0, paralelni vektor A \u003d (6, 7, -6). 7. Pronađite projekciju vektora A \u003d L + J- KHA vektor B \u003d 21 - J - 3K. 8. Pronađite kosinus ugla između je vektora, ako (-4,0,4), u (-1,6,7), C (1,10,9). 9. Pronađite jedan vektor p °, istovremeno okomito vektor A \u003d (3, 6, 8) i osi Ox. 10. Izračunajte kutni sinus između dijagonala paraleloofma, ugrađenog u vektore A \u003d 2i + J-K, B \u003d I-3J + K kao na stranama. Izračunajte visinu H Paralelepiped, ugrađen u vektore A \u003d 31 + 2J - 5K, B \u003d I-J + 4kNC \u003d I-3J + K, ako bazu uzima paralelogrami, ugrađeni u vektore A i I). Odgovori

Svojstva skalarnog komada

Skalarni proizvod vektora, definicije, svojstva

Linearno operacije preko vektora.

Vektori, osnovni pojmovi, definicije, linearne operacije na njima

Vektor u avionu naziva se naređeni par točkica, dok se prva tačka naziva početkom, a drugi kraj - vektor

Dva vektora nazivaju se jednakim ako su jednaki i suigravali.

Vektori koji leže na jednoj ravnu liniju nazivaju se uvlačenim ako su presvučeni nekim i istim vektorom ne leži na ovoj ravnoj liniji.

Vektori koji leže na jednoj ravni ili na paralelnoj direktno nazivaju se Collinear, a Collinear, ali nije umijeren - suprotno usmjereno.

Vektori koji leže na okomitim ravnim linijama nazivaju se ortogonalnim.

Definicija 5.4.. Suma a + B. vektori sVEDOK JOVANOVIĆ - ODGOVOR: i b. Nazvan vektor koji dolazi od početka vektora ali Na kraju vektora b. Ako je početak vektora b. podudara se s krajem vektora ali .

Definicija 5.5.. Razlika a - B. vektori ali i b. nazvan takav vektor od Koji u sumi sa vektorom b. daje vektoru ali .

Definicija 5.6. Raditik. sVEDOK JOVANOVIĆ - ODGOVOR: vektor ali Broj k.nazvan vektor b. , Collinear Vector ali Imati modul jednak | k.||sVEDOK JOVANOVIĆ - ODGOVOR: | i smjer se podudaraju sa smjerom ali za k.\u003e 0 i suprotno ali za k.<0.

Svojstva vektora za množenje:

Nekretnina 1. k (a + B. ) \u003d K. sVEDOK JOVANOVIĆ - ODGOVOR:+ K. b..

Nekretnina 2. (k + M)sVEDOK JOVANOVIĆ - ODGOVOR: \u003d K. sVEDOK JOVANOVIĆ - ODGOVOR:+ M. sVEDOK JOVANOVIĆ - ODGOVOR:.

Nekretnina 3. k (M. sVEDOK JOVANOVIĆ - ODGOVOR:) \u003d (km)sVEDOK JOVANOVIĆ - ODGOVOR: .

Korolija. Ako je ne-vektori ali i b. Collinear, onda postoji takav broj k., šta b \u003d. k. sVEDOK JOVANOVIĆ - ODGOVOR:.

Skalarni proizvod dva nule vektora sVEDOK JOVANOVIĆ - ODGOVOR: i b. Naziva se brojem (skalarni) jednak proizvodu dužina ovih vektora na kosinu u kut φ između njih. Scalarni proizvod može se označiti na različite načine, na primjer, kao aB, sVEDOK JOVANOVIĆ - ODGOVOR: · b., (sVEDOK JOVANOVIĆ - ODGOVOR: , b.), (sVEDOK JOVANOVIĆ - ODGOVOR: · b.). Dakle, skalarni proizvod je:

sVEDOK JOVANOVIĆ - ODGOVOR: · b. = |sVEDOK JOVANOVIĆ - ODGOVOR:| · | b.| · Cos φ.

Ako je barem jedan od vektora nula, tada je skalarni proizvod nula.

· Nekretnina permutacije: sVEDOK JOVANOVIĆ - ODGOVOR: · b. = b. · sVEDOK JOVANOVIĆ - ODGOVOR: (skalarni proizvod se ne mijenja iz preuređenja multiplikatora);

· Distributivna nekretnina: sVEDOK JOVANOVIĆ - ODGOVOR: · ( b. · c.) = (sVEDOK JOVANOVIĆ - ODGOVOR: · b.) · c. (Rezultat ne ovisi o redoslijedu množenja);

· Kombinovana nekretnina (u odnosu na skalarni faktor): (λ sVEDOK JOVANOVIĆ - ODGOVOR:) · b. = λ ( sVEDOK JOVANOVIĆ - ODGOVOR: · b.).

· Nekretnina ortogonalnosti (okomitost): ako vektor sVEDOK JOVANOVIĆ - ODGOVOR: i b. Non-Zero, njihov skalarni proizvod je nula, samo kad su ti vektori pravokutni (okomit jedni na drugi) sVEDOK JOVANOVIĆ - ODGOVOR: ┴ b.;

· Skrenite nekretnine: sVEDOK JOVANOVIĆ - ODGOVOR: · sVEDOK JOVANOVIĆ - ODGOVOR: = sVEDOK JOVANOVIĆ - ODGOVOR: 2 = |sVEDOK JOVANOVIĆ - ODGOVOR:| 2 (skalarni proizvod vektora je jednak kvadratu njegovog modula);

· Ako vektori koordiniraju sVEDOK JOVANOVIĆ - ODGOVOR:\u003d (x 1, y 1, z 1) i b.\u003d (x 2, y 2, z 2), a zatim skalarni proizvod jednak sVEDOK JOVANOVIĆ - ODGOVOR: · b. \u003d x 1 x 2 + y 1 y 2 + z 1 z 2.

Vektorski holding vektori. Definicija: Pod vektorskim proizvodom dva vektora i razumije se kao vektor za koji:

Modul je jednak području paralelograma izgrađenog na podacima vektora, I.E. gdje kut između vektora i

Ovaj vektor je okomit na varijable vektore, i.e.

Ako su vektori neullyline, onda formiraju ispravna tri vektora.

Svojstva vektorskog rada:

1. Prilikom promjene redoslijeda faktora, vektorski proizvod mijenja znak na suprotno, uštedu modula, I.E.

2 Trg .Vector je nula-vektor, i.e.

3 . Potpuni multiplikator može se napraviti za vektorski rad, I.E.

4 . Za svaka tri vektora sajamna ravnopravnost

5 . Eugene i dovoljan uvjet za kolibranost dva vektora i:

Očito, u slučaju vektorskog rada, naredba u kojem se vektor uzima, osim toga,

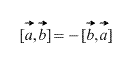
Također, direktno iz definicije slijedi da je za bilo koji skalarni multiplikator k (broj) sljedeće istina:

Vektorski proizvod Collinear vektora jednak nulti vektora. Štaviše, vektorski proizvod dva vektora je nula ako i samo ako su kolinore. (U slučaju da se jedan od njih nula vektor mora podsjećati da se nulti vektor kolinira u bilo kojem vektoru po definiciji).

Vektorski rad poseduje distributivna imovina, i.e

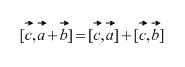
Izraz vektorske umjetnosti kroz koordinate vektora.

Neka se daju dvije verzije

(Kako pronaći koordinate vektorskih koordinata svog početka i kraja - pogledajte članak skalarnog proizvoda vektora, alternativna definicija skalarnog proizvoda ili izračunavanje skalarnog proizvoda dva vektora navedene u njenim koordinatama.)

Zašto mi treba vektorski rad?

Mnogo je načina da se primijeni vektorski proizvod, na primjer, kao što je već napisano gore, izračun vektorskog proizvoda dva vektora može se saznati da li su kolinore.

Ili se može koristiti kao metoda za izračunavanje paralelogramskog područja izgrađenog na ovim vektorima. Na osnovu definicije, dužina rezultirajućeg vektora je područje ovog paralelograma.

Takođe, u električnoj energiji i magnetizmu postoji ogromna količina prijava.

Online vektorski umjetnički kalkulator.

Da biste pronašli skalarni proizvod dva vektora pomoću ovog kalkulatora, morate ući u prvu retku kako bi se koordinata prvog vektora, u drugom drugom. Koordinate vektora mogu se izračunati koordinatama njihovog početka i kraja (vidi članak Scalarni proizvod vektora, alternativna definicija skalarnog proizvoda ili izračunavanje skalarnog proizvoda dva vektora navedena prema njenim koordinatama.)